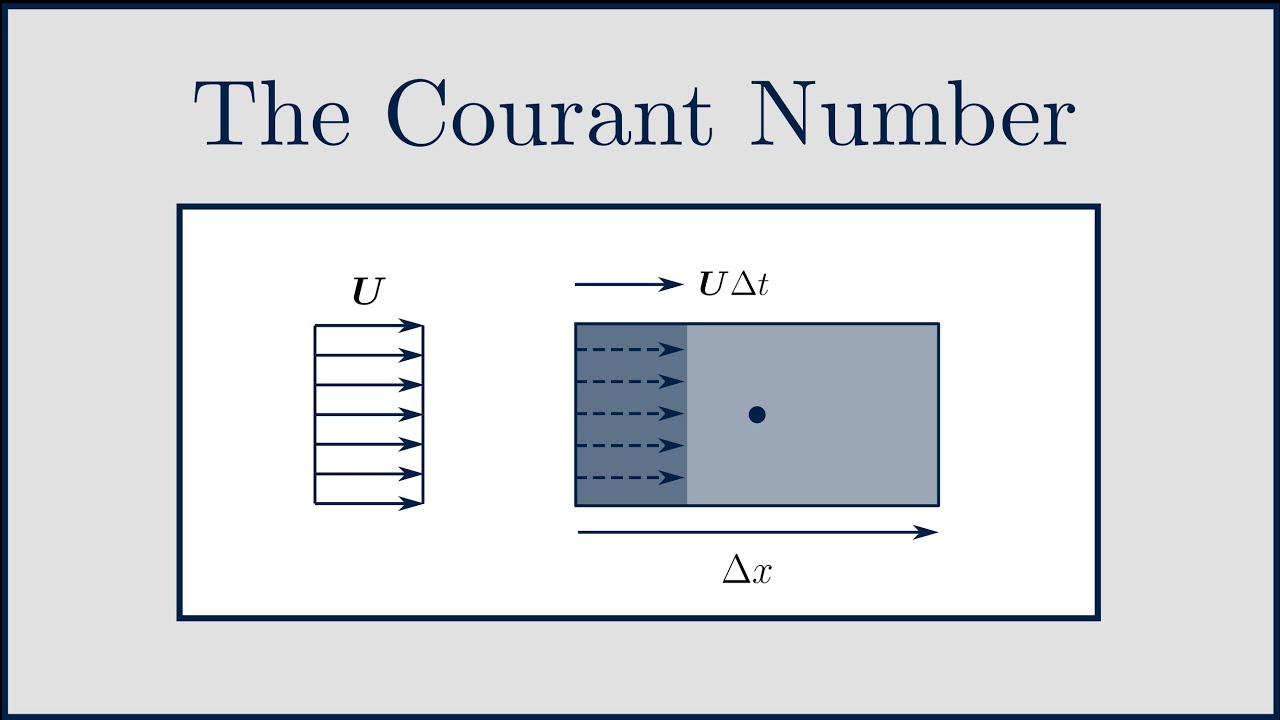
The Courant-Friedrichs-Lewy condition, sometimes called the CFL condition, is concerned with how far any information goes inside the mesh at a given time step. The Courant number is calculated using the following formula, derived from the CFL condition:
C=uΔt/Δx
C is the Courant number, u is the magnitude of the velocity, t is the size of the time step, and x is the distance between the mesh elements.
It is a dimensionless parameter that arises in numerical simulations of partial differential equations, particularly in the context of hyperbolic equations like the wave equation and the transport equation.
Besides, you can regulate the courant number by changing the time or space interval. The courant number grows when the space or time intervals are stretched out. It is crucial to set the intervals carefully since the courant number controls how stable an issue is when using an explicit technique.
Why is the Courant number significant?
The Courant number is important because it affects the numerical system’s stability and accuracy. It provides information about the flow of fluid via your computational cells. In particular, the Courant number must be less than or equal to a specific value (typically 1) for the numerical solution to be stable and converge to the correct answer. The too large courant number has a detrimental impact on convergence.
What actually does a courant number do?
The CFL condition appears in the generic partial differential equations that approximate finite differences and control the advection phenomena. The velocity, time step, and distance between two nodes are all crucial factors in an explicit time marching issue, such as a one-dimensional wave motion. The Courant number does not appear in steady-state problems and primarily controls a numerical method’s stability in transient equations. Its buildup isn’t only limited to one-dimensional issues. It can also happen in two-dimensional cases. For a limited number of dimensions, there can be a finite number of courant digits. Problems, in reality, are only three-dimensional. Hence there can only be a maximum of three courant numbers.
The CFL condition and courant number?
The CFL (Courant-Friedrichs-Lewy) condition is a numerical stability criterion
for solving partial differential equations (PDEs) numerically.
The CFL condition states that for a numerical scheme to be stable, the time step used in the simulation must be small enough so that the distance a wave can travel during a one-time phase is less than the distance between adjacent grid points. Mathematically, the CFL condition can be expressed as:
Δt ≤ C Δx / v
where Δt is the time step, Δx is the grid spacing, v is the velocity of the wave being simulated, and C is the Courant number.
As said earlier, the Courant number measures how quickly a wave moves across a grid cell relative to the time step.
The value of the Courant number should be less than or equal to 1 for stability. A Courant number greater than 1 implies that the wave can travel more than one grid cell during a time step, leading to numerical instability and inaccurate results.
Conclusion
In summary, the CFL condition and the Courant numbers are essential concepts in numerical simulations of PDEs. They ensure the stability and accuracy of the numerical scheme used in the simulation.